Kelly Criterion and Optimal Betting Strategy

John L. Kelly Jr. is credited with developing the foundational concept of logarithmic utility maximization in gambling and repeated investment scenarios—a framework now universally known as the Kelly criterion. Kelly's seminal work established two fundamental results: first, that logarithmic utility functions maximize the asymptotic growth rate of capital, and second, that this approach exhibits a "myopic" optimality property, wherein period-by-period optimization based solely on current wealth is sufficient for achieving long-term optimal growth. These insights have profound implications for portfolio theory, risk management, and quantitative finance.

Mathematical Foundations

The Single-Asset Case

Consider a sequence of Bernoulli trials representing independent investment opportunities, where the investor wins with probability $p$ and loses with probability $q = 1 - p$. Let $B$ denote the odds ratio—the units gained per unit wagered upon success. Kelly demonstrated that maximizing the long-run growth rate of wealth is equivalent to maximizing the expected logarithm of single-period returns.

For a wager of fraction $f$ of total capital $W$, the expected logarithmic growth rate is given by:

$$g(f) = \mathbb{E}[\log W'] = p \log(1 + Bf) + q \log(1 - f)$$

Differentiation yields the optimal fraction:

$$f^\star = \frac{Bp - q}{B} = \frac{\text{edge}}{\text{odds}}$$

where $Bp - q$ represents the expected value per unit wagered. This elegant result reveals that optimal position sizing is simply the ratio of edge to odds. Crucially, this criterion maximizes geometric rather than arithmetic mean returns, thereby avoiding the pitfall of ruin inherent in strategies that maximize expected value without regard to variance.

Theoretical Justification for Logarithmic Utility

The adoption of logarithmic utility is not arbitrary but derives from the principle of constant relative risk aversion (CRRA). Under this framework, the marginal utility of wealth is inversely proportional to current wealth:

$$U'(W) \propto \frac{1}{W} \implies U(W) = \log W$$

This specification implies that agents exhibit identical concern for proportional changes in wealth regardless of their absolute wealth level—a property with strong empirical and axiomatic support in decision theory. The logarithmic function uniquely satisfies this criterion while maintaining analytical tractability.

Extension to Multiple Simultaneous Wagers

Favorable Games and General Formulation

Edward O. Thorp and subsequent researchers have extended Kelly's framework to scenarios involving simultaneous bets on multiple events. We first define favorable games as those admitting strategies satisfying:

$$P\left( \lim_{N \rightarrow \infty} W_N > 0 \right) = 1$$

where $W_N$ denotes capital after $N$ trials. This condition ensures that with optimal strategy, the probability of maintaining positive capital approaches certainty as the number of trials increases.

Consider $n$ concurrent wagers with betting fractions $\mathbf{f} = (f_1, \ldots, f_n)$. Let $\mathbf{x} = (x_1, \ldots, x_n)$ denote the outcome vector, where $x_i = B_i$ (the odds) upon success and $x_i = -1$ upon failure for the $i$-th wager. The expected logarithmic growth rate is then:

$$g(\mathbf{f}) = \sum_{\mathbf{x}} P(\mathbf{x}) \log\left(1 + \mathbf{f} \cdot \mathbf{x}\right)$$

where $P(\mathbf{x})$ is the joint probability distribution over all possible outcome configurations and $\mathbf{f} \cdot \mathbf{x} = \sum_i f_i x_i$ represents the total return.

Optimization and Correlation Effects

Determining the optimal fractions $\mathbf{f}^\star$ requires solving the system of first-order conditions $\nabla g(\mathbf{f}) = \mathbf{0}$ subject to the constraint that total exposure does not exceed available capital. In practice, sequential quadratic programming (SQP) or interior-point methods provide robust numerical solutions.

A critical insight emerges from this analysis: optimal fractions for simultaneous wagers are generally smaller than those computed by treating each bet in isolation. Furthermore, when betting on correlated markets within the same event—such as wagering on both the winner and total score of a single game—ignoring dependence structure can lead to substantial deviations from true optimality. Accurate determination of optimal fractions requires knowledge of the complete joint probability distribution, not merely pairwise correlations.

Strategic Considerations

Hedging and Risk Mitigation

An important extension of the Kelly framework involves hedging—the strategic combination of positions where expected returns aggregate while risks partially offset. This technique proves particularly valuable when strong negative correlations exist between available opportunities. A risk-averse investor can construct portfolios exhibiting superior risk-adjusted growth by exploiting such correlation structures.

Arbitrage Detection

Numerical optimization of the Kelly objective function over mutually exclusive outcomes automatically identifies and exploits arbitrage opportunities—situations where guaranteed profit is achievable regardless of the realized outcome. However, practical implementation faces challenges including execution risk, price slippage, and counterparty risk from potential bet cancellation.

Empirical Performance

Monte Carlo simulation provides compelling evidence for the superiority of properly calibrated Kelly strategies. Comparative studies demonstrate that strategies accounting for the full joint distribution of outcomes substantially outperform those based on sequential single-bet optimization.

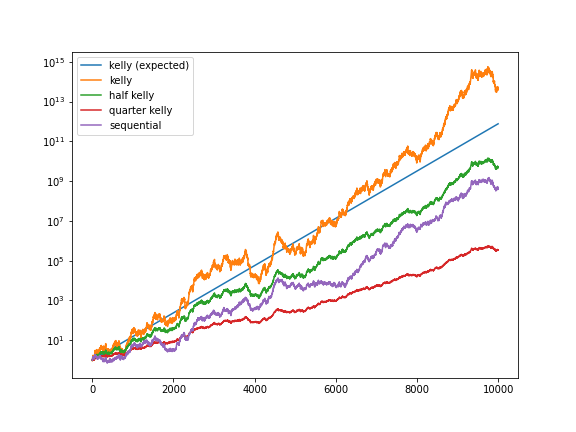
The logarithmic scale of these simulations reveals the compounding advantage of optimal capital allocation over extended time horizons.

Practical Implementation: Fractional Kelly

While theoretically optimal, full Kelly sizing induces substantial volatility and drawdown risk. Moreover, estimation error in edge parameters compounds over time, potentially leading to systematic overbetting. To address these concerns, practitioners commonly employ fractional Kelly strategies, betting a fixed proportion $\lambda \in (0, 1)$ of the recommended Kelly fraction.

This conservative modification permits explicit control over the risk-return tradeoff: half-Kelly ($\lambda = 0.5$) achieves approximately 75% of the full Kelly growth rate while halving variance, whereas quarter-Kelly ($\lambda = 0.25$) provides a more robust buffer against parameter uncertainty. The selection of $\lambda$ reflects the investor's confidence in edge estimates and tolerance for interim volatility.